homeyou

Original Article: Tropical Interpolation

Author: Frank Sottile

Interpolação Trópical

   Todos sabem que dois pontos determinam uma linha, e muitas das pessoas que estudaram geometria sabem que cinco pontos em um plano determinam uma cônica. Em geral, se você tem m pontos aleatórios no plano e você quer passar uma curva racional de grau d por todos eles, pode não haver qualquer solução para esse problema de interpolação (se m for muito grande), ou um infinito número de soluções (se m for muito pequeno), ou um número de soluções finito (se m for perfeito). Acontece que ‘m perfeito’ corresponde a m=3d-1 (m=2 para linhas e m=5 para cônicas).

   Uma questão mais difícil seria, se m=3d-1, quantas curvas racionais de grau d interpolam os pontos? Vamos chamá-lo de Nd, para que N1=1 e N2=1, pois a linha e a cônica do parágrafo anterior são únicas. Há muito sabe-se que N3=12, e em 1873 Zeuthen [Ze] mostrou que N4=620. Foi aí em que os fatos perduraram até mais ou menos dez anos atrás, quando Kontsevich e Manin [KM] usaram associatividade em co-homologia quântica a fim de dar uma recursão elegante para esse número.

   Os temas de pesquisa no semestre de inverno de 2004 do MSRI sobre Aspectos Topológicos de Geometria Algébrica Real incluíram geometria algébrica real enumerativa, geometria tropical, planos curvos reais, e aplicações de geometria algébrica real. Todos estão interligados no desdobramento da estória desse problema de interpolação, um problema prototípico de geometria enumerativa, a qual é a arte de contar figuras geométricas determinadas por certas condições de incidência. Aqui está outro problema: quantas linhas no espaço encontram quatro linhas dadas? Para respondê-lo, perceba que três linhas encontram-se em uma única hiperbolóide dupla.

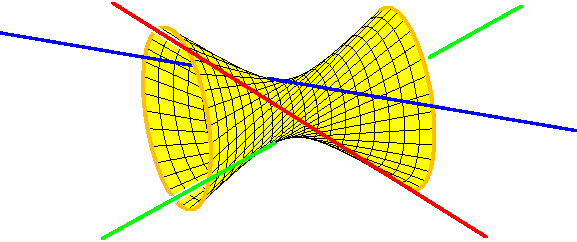
As três linhas encontram-se em uma dirigente, e a segunda dirigente consiste das linhas que encontram as três linhas dadas. Sendo que a hiperbolóide é definida por uma equação quadrática, uma quarta linha encontrá-la-á em dois pontos. Em cada um desses dois pontos existe uma linha na segunda dirigente, e essas são as duas linhas que encontram as nossas quatro linhas dadas.

   Geometria enumerativa funciona melhor com números complexos, enquanto o número de figuras reais depende bastante sutilmente na configuração das figuras que ditam as condições de incidência. Por exemplo, a quarta linhas pode encontrar a hiperbolóide em dois pontos reais, ou em dois pontos complexos conjugados, então existe duas ou nenhuma linha real encontrando todas as quatro. Baseado em múltiplos exemplos, viemos a esperar que um problema enumerativo pode apresentar todas as soluções como sendo reais. [So].

   Outro problema são as 12 curvas racionais interpolando 8 pontos no plano. A maioria dos matemáticos estão familiarizados com o nodal cúbico (racional) mostrado abaixo à esquerda. Existe outro tipo de cúbico real racional, à direita.

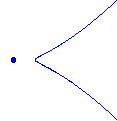
Na segunda curva, duas ramificações complexas conjugadas se encontram em um ponto isolado. Se deixarmos N(t) ser o número de curvas reais de tipo t interpolando em 8 dados pontos, então Kharlamov e Degtyarev mostram que

N( ) – N( ) = 8 .”

Aqui está uma descrição dos métodos elementares topológicos.

   Já que existem no máximo 12 curvas dessa forma, N( ) – N( ) \ led 12, então existem 8, 10 ou 12 cúbicos reais racionais interpolando 8 pontos reais no plano, dependendo no número (0, 1 ou 2) de cúbicos com um ponto isolado. Dessa forma haverá então 12 cúbicos reais racionais interpolando qualquer 8 dos 9 pontos de interseção dos dois cúbicos abaixo.

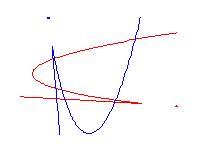
   Welschinger [W], que era um pós-doutor MSRI no inverno passado, desenvolveu este exemplo em uma teoria. Em geral, as singularidades de um plano curvo real racional C são nódulos ou pontos isolados. A paridade de números de nodos está no seu sinal S©, o qual é ou 1 ou -1. Dados 3d-1 pontos reais no plano, Welschinger considerou o valor absoluto da quantidade

s( C ) ,

a soma sobre todas as curvas reais racionais C de grau d que interpolam os pontos. Ele mostrou que esta soma não depende na escolha dos pontos. Escreva Wd para esta invariante de Welschinger. Por exemplo, já vimos que W3=8.

   Isto foi uma descoberta, já que Wd era (quase) a primeira verdadeira invariante não-trivial em geometria algébrica enumerativa real. Perceba que Wd é um limite mais inferior para o número de curvas reais racionais através de 3d-1 pontos reais no plano, e Wd\leq Nd

    Mikhalkin, que foi o organizador do semestre, forneceu a chave para computar Wd usando geometria algébrica trópica [Mi]. Esta é a geometria dos semi-anéis trópicos, onde as operações de máx e + em números reais substituem as operações usuais de + e multiplicação. Um polinômio trópico é uma fatia da função linear da forma

onde o cálculo está conjunto com as operações aritméticas usuais e o máximo é extraído de um subgrupo finito de Z2 de exponentes de T e ci,j como os números coeficientes reais de T. Um polinômio trópico T define a curva trópica, o qual é o grupo de pontos (x,y), onde T(x,y) não é diferenciável. Aqui estão algumas curvas trópicas.

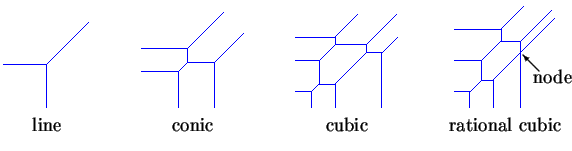
O grau de uma curva trópica é o número de raios que tendem ao infinito seja em três das direções Oeste, Sul, ou Nordeste. Uma curva trópica é racional se a mesma é uma imersão de uma fatia linear de uma árvore. Nódulos têm valência 4.

    Mikhalkin mostrou que somente existem finitamente muitas curvas racionais trópicas de grau d interpolando pontos genéricos 3d-1. Enquanto o número de tais curvas depende da escolha de pontos, Mikhalkin anexou multiplicidades positivas para cada curva trópica para que a soma não dependa, e seja de fato igual a Nd. Ele também reduziu estas multiplicidades e a enumeração de curvas trópicas para as combinatórias de vias estruturadas dentro de um triângulo de comprimento d.

    Mikhalkin usou uma correspondência envolvendo o mapa Log:(C*)2 —> R2 definido por (x,y)|—>(log|x|,log|y|), e um certo “limite extenso complexo” da estrutura complexa em (C*)2. Sob este limite extenso complexo, aquelas imagens sob Log são curvas trópicas normais interpolando as imagens dos pontos. A multiplicidade de uma curva trópica T é o número de curvas trópicas complexas que projetam a T.

    E que tal curvas reais? Seguindo esta correspondência, Mikhalkin anexou a multiplicidade real para cada curva trópica e mostrou que se as curvas trópicas interpolando um dado ponto 3d-1 têm uma multiplicidade total real N, então há 3d-1 pontos reais que são interpolados por N curvas reais racionais de grau d. Esta multiplicidade real é novamente expressada em termos de vias estruturadas.

    E o invariante de Welschinger? Da mesma forma, Mikhalkin atribuiu um peso assinado a cada curva tropical (uma versão tropical do sinal de Welschinger) e mostrou que a soma ponderada correspondente equivale ao invariante de Welschinger. Como antes, este peso assinado tropical pode ser expresso em termos de caminhos de rede.

    Durante o semestre em MSRI, Itenberg, Kharlamov, e Shustin [IKS] usaram os resultados de Mikhalkin para estimar invariantes Welschinger. Foi verificado que Wd\geq d!/3, e também

Então pelo menos logaritmicamente, a maioria das curvas racionais de grau d interpolando pontos 3d-1 reais no plano são reais.

    Existem duas outras instâncias deste fenômeno de limites inferiores, dos quais os primeiros pré-datam o trabalho de Welschinger. Suponha que d é constante e deixe W(s) ser um polinômio real de grau k(d-k+1). Então Eremenko e Gabrielov [EG] mostram que existem polinômios reais f1(s),…, fk(s) de grau d os quais a determinante Wronski é W(s). De fato, eles provam um limite inferior no número de k-duplos de polinômios, até uma equivalência. Similarmente, enquanto em MSRI, Soprunova e I [SS] estudaram sistemas de polinômios esparsos associados a grupos parcialmente ordenados. Tais limites inferiores para problemas enumerativos, os quais implicam a existência de soluções reais, são importantes para aplicações.

    Por exemplo, esta estória foi recontada em um happy-hour uma noita na Workshop MSRI sobre Modelos Geométricos e Geometria Algébrica Real em Abril de 2004. Um participante, Schicho, se deu conta de que o resultado W3=8 para cúbicos explica porque o método que ele tinha desenvolvido sempre parecia funcionar. Este era um algoritmo para computar uma parametrização aproximada da arca de uma curva, via um cúbico real racional interpolando 8 pontos na arca. Ficou em aberto encontrar condições que garantam a existência de uma solução que seja próxima à arca. Isto foi recentemente resolvido por Fiedler-Le Touzé, um pós-doutor MSRI que havia estudado cúbicos (não necessariamente racionais) interpolando 8 pontos para ajudar classificar planos curvos reais de grau 9.

Bibliografia

• [DK] A. I. Degtyarev e V. M. Kharlamov, Propriedades topológicas de variedades algébricas reais: Caminho de Rokhlin, Uspekhi Mat. Nauk 55 (2000), no. 4 (334), 129-212.
• [EG] A. Eremenko e A. Gabrielov, graus de mapas reais de Wronski, Discrete Comput. Geom. 28 (2002), no. 3, 331 – 347.
• I. Itenberg, V. Kharlamov e E. Shustin, equivalência logarítmica dos invariantes Welschinger e Gromov-Witten arXiv: math.AG / 0407188.
• [KM] M. Kontsevich e Yu. Manin, aulas de Gromov-Witten, cohomologia quântica e geometria enumerativa, Comm. Matemática. Phys. 164 (1994), no. 3, 525-562.
• [Mi] G. Mikhalkin, geometria algébrica trópica enumerativa em R2, arXiv: math.AG/0312530.
• [SS] E. Soprunova e F. Sottile, Lower Bounds para soluções reais para sistemas polinomiais dispersos, arXiv: math.AG/0312530.
• [So] F. Sottile, geometria algébrica real enumerativa, geometria algébrica real algorítmica e quantitativa (Piscataway, NJ, 2001), DIMACS Ser. Matemática discreta. Theoret. Comput. Sci., Vol. 60, Amer. Matemática. Soc., Providence, RI, 2003, pp. 139—179.
• [W] J.-Y. Welschinger, invariantes de 4 variedades verdadeiramente racionais simplistas e limites inferiores em geometria enumerativa real, C. R. Math. Acad. Sci. Paris 336 (2003), no. 4, 341 – 344.
• [Ze] H. G. Zeuthen, Almindelige Egenskaber ved Systemer af plane Kurver, Danske Videnskabernes Selskabs Skrifter, Naturvidenskabelig og Mathematisk, Afd. 10 Bd. IV