Author: Philip J. Erdelsky
|
Um pedaço de πPhilip J. Erdelsky26 de julho de 2001 |
Por favor envie comentários, correções e acréscimos para o e-mail do webmaster em [email protected].
Matemática contém muitas constantes transcendentais interessantes, mas apenas uma delas era conhecido pelos antigos. É π, a proporção entre a circunferência e o diâmetro de um círculo.
Arquimedes foi o primeiro matemático para calcular um valor aproximado para π. Valores anteriores foram baseadas em medições físicas de precisão limitada.
Vamos usar o método de Arquimedes para calcular um valor aproximado de π, utilizando apenas matemática conhecida por Arquimedes. No entanto, estaremos fazendo nossos cálculos em um computador, e vamos obter um valor muito mais preciso do que ele obteve.
Os antigos não tinham uma boa teoria de limites; nem a maioria dos não-matemáticos. Mas algumas coisas são bastante óbvias. Um polígono regular com muitos lados é aproximadamente um círculo. O seu perímetro é aproximadamente a circunferência do círculo, e a sua área é, aproximadamente, a área do círculo. Quanto mais lados o polígono tem, mais precisa será a aproximação. Se o polígono tem lados suficientes, pode ser obtido qualquer grau desejado de precisão.
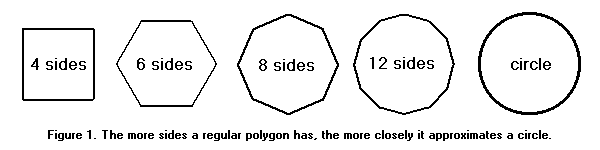
Para encontrar um valor aproximado para π, vamos inscrever polígonos regulares em um círculo de raio 1. Os perímetros dos polígonos podem ser calculado em alguns casos, usando nada mais avançado do que o teorema de Pitágoras, que era conhecido por Arquimedes. Em particular, se sabemos o comprimento de cada lado do polígono regular com n lados, podemos calcular o comprimento de cada lado do polígono regular com 2n lados.
Na Figura 2, deixe AB ser um dos n lados de um polígono regular inscrito num círculo com centro em O e raio de uma unidade. Seja s o comprimento de AB.
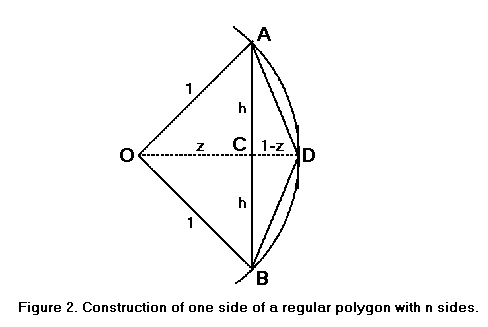
Deixe OCD ser a bissetriz do ângulo AOB. Então triângulos AOC e BOC são congruentes; portanto, os ângulos C são ângulos retos e AC = CB. Portanto,
- h = s/2
- z = √(1-h2)
O perímetro do polígono é ns e o diâmetro do círculo é 2.Por isso, o valor aproximado de π é NS /2.
Os segmentos de linha de AD e BD são os lados de um polígono inscrito com 2n lados. O comprimento de cada um é
- √(h2 + (1-z)2))
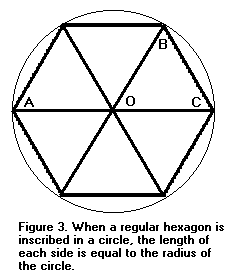
No caso onde n =6, sabemos que s =1. Este é um fato bem conhecido, mas vamos dar uma pequena prova. Já que o hexágono é regular, todos os seis ângulos no centro são iguais. O ângulo ACB está inscrita num círculo, por isso, é a metade do ângulo interceptado AOB, o qual é igual a dois dos seis ângulos. Assim o ângulo ACB é igual ao ângulo BOC. Os lados opostos de OB e BC também são iguais. Argumentos semelhantes mostram todos os outros lado tão longos quanto o raio do círculo.
Tudo o que temos a fazer é aplicar esta fórmula repetidamente para obter valores para n = 12, 24, 48, 96, etc.
Um programa de computador simples, como o seguinte programa C ++, irá realizar esses cálculos rapidamente.
#include <stdio.h>
#include <math.h>
void main(void)
{
double s = 1.0;
double n = 6.0;
puts("number of sides approximate value of pi");
while (n < 500000000.0)
{
printf ("%9.0f %18.16f\n", n, n*s/2.0);
double h = s / 2.0;
double z = sqrt(1.0 - h * h);
s = sqrt(h * h + (1.0 - z) * (1.0 - z));
n *= 2;
}
}
Os resultados se parecem com:
Número de lados Valor aproximado de pi
6 3.0000000000000000
12 3.1058285412302489
24 3.1326286132812378
48 3.1393502030468667
96 3.1410319508905098
192 3.1414524722854624
384 3.1415576079118579
768 3.1415838921483186
1536 3.1415904632280505
3072 3.1415921059992717
6144 3.1415925166921577
12288 3.1415926193653840
24576 3.1415926450336911
49152 3.1415926514507682
98304 3.1415926530550373
196608 3.1415926534561045
393216 3.1415926535563719
786432 3.1415926535814380
1572864 3.1415926535877046
3145728 3.1415926535892713
6291456 3.1415926535896630
12582912 3.1415926535897611
25165824 3.1415926535897856
50331648 3.1415926535897913
100663296 3.1415926535897931
201326592 3.1415926535897931
402653184 3.1415926535897931
Arquimedes, com nada melhor do que um ábaco para computar com, teve que parar em 96 lados.

